Ovo je stara izmjena dokumenta!
Sadržaj
Kriptografija javnog ključa
1. Sažetak
2. Uvod – što je to kriptografija?
Kriptografija je znanstvena disciplina koja se bavi proučavanjem metoda koje se koriste za slanje poruka, tj. informacija u obliku koji je razumljiv samo onima kojima su te poruke namijenjene. Naziv dolazi od grčkih riječi kriptós što znači skriven i gráfo što znači pisati. Razvoj kriptografije potaknut je činjenicom da se prijenos informacija često odvija putem nesigurnih komunikacijskih kanala (slika 1).

Slika 1: Nesigurni komunikacijski kanal
Zbog toga je potrebno na neki način zaštititi informacije koje se prenose tako da nitko osim osoba kojima su te informacije namijenjene ne može doći do njih. Kriptografija se upotrebljava u mnogim segmentima ljudskog života kao što su autentifikacija, enkripcija email-ova, enkripcija WhatsApp poruka, itd.
3. Kriptografija - osnovni pojmovi
Kriptografija kao i svaka znanstvena disciplina radi jednostavnosti komunikacije koristi stručne pojmove. Definirajmo osnovne pojmove u kriptografiji koji će se koristiti u sljedećim poglavljima.
Pošiljatelj je osoba koja šalje poruku, a primatelj je osoba koja tu poruku prima. Cilj kriptografije je omogućiti izmjenu poruka između pošiljatelja i primatelja koja se odvija na način da neka treća osoba, koju nazivamo protivnik, ne može pročitati njihove poruke.
Otvoreni tekst naziv je koji se odnosi na poruku koja se šalje, a šifrat je naziv koji se odnosi na oblik u kojem je ta poruka zapisana, tj. oblik u kojem će primatelj dobiti tu poruku. Šifriranje je postupak preobrazbe otvorenog teksta u šifrat. Šifriranje provodi pošiljatelj pomoću unaprijed definiranog ključa.
Izmjena informacija između pošiljatelja i primatelja (slika 2) odvija se komunikacijskim kanalom. Protivnik može doći do šifrata, ali ne može ga dešifrirati i doći do otvorenog teksta zato što nema ključ kojim je otvoreni tekst šifriran.
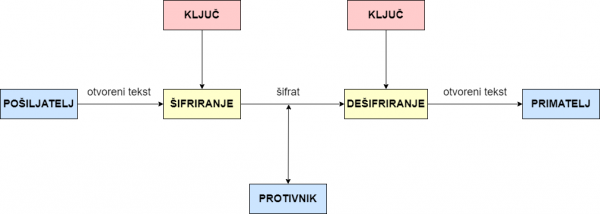
Slika 2: Izmjena poruka između pošiljatelja i primatelja
Kriptografski algoritam je matematička funkcija koja se koristi za šifriranje i dešifriranje. Obično su to dvije funkcije od kojih jedna preslikava elemente otvorenog teksta u elemente šifrata, a druga preslikava elemente šifrata u otvoreni tekst.
Kriptosustav je uređena petorka (P, C, K, E, D) za koju vrijedi:
- P predstavlja konačan skup svih mogućih osnovnih elemenata otvorenog teksta.
- C predstavlja konačan skup svih mogućih osnovnih elemenata šifrata.
- K predstavlja prostor ključeva (konačan skup svih mogućih ključeva).
- E predstavlja skup svih mogućih funkcija šifriranja.
- D predstavlja skup svih mogućih funkcija šifriranja.
- Za svaki K ∈ K postoji funkcija šifriranja eK ∈ E i odgovarajuća funkcija dešifriranja dK ∈ D . Pri tome su eK : P → C i dK : C → P funkcije za koje vrijedi da je dK(eK(x)) = x za svaki otvoreni tekst x ∈ P.
4. Podjela kriptosustava
Kriptosustavi su uobičajeno klasificirani s obzirom na tri kriterija:
- Tip operacije koja se koristi pri šifriranju: Podjela na supstitucijske (svaki element otvorenog teksta zamijeni se nekim drugim elementom), transpozicijske (napravi se permutacija otvorenog teksta) i šifre koje su njihova kombinacija.
- Način na koji se obrađuje otvoreni tekst: Podjela na blok šifre (jedan po jedan blok elemenata otvorenog teksta obrađuje se pomoću istog ključa) i protočne šifre (jedan po jedan element otvorenog teksta obrađuje se pomoću niza ključeva).
- Tajnost ključeva: Podjela na kriptosustave s javnim ključem, tj. asimetrične kriptosustave (ključ za šifriranje je javan, a ključ za dešifriranje ima samo osoba koja treba dešifrirati poruku) i kriptosustave s tajnim ključem, tj. simetrične kriptosustave (ključ za šifriranje je tajan, a često su ključ za šifriranje i ključ za dešifriranje jednaki).
5. Kriptografija javnog ključa
Kriptografija javnog ključa naziva se i asimetrična kriptografija, a naziv se temelji na činjenici da takav sustav koristi par ključeva koji se sastoji od javnog i privatnog ključa. Sigurnost asimetrične kriptografije temelji se na očuvanju privatnog ključa tajnim. Otvoreni tekst se šifrira s javnim ključem, a šifrat se dešifrira s privatnim ključem. Slika 3 prikazuje jednostavni kriptosustav s javnim ključem koji je pohranjen u neku javnu datoteku koja je svima dostupna.
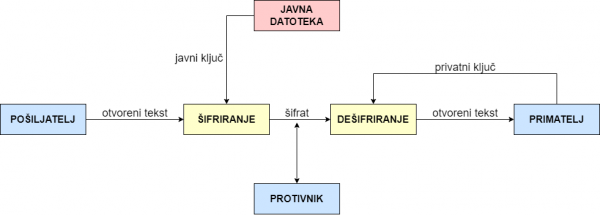
Slika 3: Jednostavni kriptosustav s javnim ključem
Koristeći javni ključ bilo tko može šifrirati otvoreni tekst, ali šifrat može dešifrirati samo osoba kojoj je dostupan privatni ključ. Privatni ključ za dešifriranje mora biti takav da ga protivnik ne može izračunati u razumnom vremenu ako mu je dostupan javni ključ za šifriranje. Ako bilo tko može doći do javnog ključa i predstaviti se kao pošiljatelj, postavlja se pitanje je li poslani šifrat vjerodostojan i autentičan. To pitanje može se riješiti na način da pošiljatelj generira neki slučajan broj a kojeg doda svojoj poruci koju šalje primatelju. Zatim primatelj generira neki slučajni broj b koji zbroji s a te taj zbroj šifrira s javnim ključem i pošalje ga pošiljatelju. Pošiljatelj dešifriranjem dobivenog šifrata privatnim ključem dolazi do zbroja a+b. Oduzimanjem svog slučajnog broja a od dobivenog zbroja dobiva primateljev slučajni broj b. Svakoj sljedećoj poruci pošiljatelj dodaje b, a primatelj provjerava je li poslani b jednak njegovom slučajnom broju b.
Glavne prednosti kriptosustava s javnim ključem su da nema potrebe za sigurnim komunikacijskim kanalom za razmjenu javnih ključeva, javni i privatni ključ mogu se koristiti određeni period vremena dok se kod simetričnih sustava novi ključevi moraju redovito generirati te postoji mogućnost potpisa poruke što omogućava da pošiljatelj ne može tvrditi da nije poslao neku poruku ako se na njoj nalazi njegov potpis. Glavni nedostaci kriptosustava s javnim ključem su da je značajno sporiji od kriptosustava s tajnim ključem te da su ključevi asimetričnih sustava značajno veći od ključeva simetričnih sustava. U praksi se kriptosustavi s javnim ključem koriste za šifriranje ključeva, a ne za šifriranje poruka.
6.Primjeri kriptosustava koji koriste javni ključ
U ovom poglavlju bit će opisani najpoznatiji kriptosustavi koji koriste metodu javnog ključa.
6.1 RSA kriptosustav
RSA kriptosustav funkcionira na temelju generiranja velikih prostih brojeva. Algoritam za generiranje javnog i privatnog ključa za RSA kriptosustav glasi:
- Potrebno je generirati dva velika prosta broja p i q.
- Na temelju p i q se izračunava n=pq i φ(n) = (p - 1)(q - 1).
- Slučajno se odabire se cijeli broj e koji je relativno prost sa φ(n) (njihov najveći zajednički djelitelj je jednak 1) za koji vrijedi 1 < e < φ(n).
- Na temelju formule ed ≡ 1 (mod φ(n)) se izračuna d za koji vrijedi 1 < d < φ(n).
- Javni ključ je (n, e), a privatni ključ je d.
Algoritam za RSA šifriranje otvorenog teksta javnim ključem glasi:
- Potrebno je dohvatiti javni ključ (n, e).
- Poruka se prikaže kao cijeli broj x.
- Šifrat se izračuna pomoću formule eK(x) ≡ x^e (mod n).
- Šifrat se pošalje primatelju.
Algoritam za RSA dešifriranje šifrata privatnim ključem glasi:
- Element brojane listePotreban je privatni ključ d.
- Otvoreni tekst se izračuna pomoću formule dK(y) ≡ y^d (mod n).
Radi boljeg razumijevanja načina funkcioniranja RSA kriptosustava u tablici 1 je prikazano nekoliko primjera generiranja ključeva, šifriranja i dešifriranja u RSA kriptosustavu. Radi jednostavnosti i preglednosti p i q su mali prosti brojevi. Kao što se može vidjeti, poruke x jednake su vrijednosti kao i dešifrirani šifrat dK.
| p | q | n | φ(n) | e | d | x | eK | dK |
| 3 | 5 | 15 | 8 | 3 | 3 | 2 | 8 | 2 |
| 5 | 11 | 55 | 40 | 3 | 27 | 2 | 8 | 2 |
| 11 | 17 | 187 | 160 | 3 | 107 | 2 | 8 | 2 |
Tablica 1: Primjer šifriranja u RSA kriptosustavu
6.2 Rabinov kriptosustav
Rabinov kriptosustav također koristi generiranje velikih prostih brojeva. Algoritam za generiranje javnog i privatnog ključa za Rabinov kriptosustav glasi:
- Potrebno je generirati dva velika prosta broja p i q.
- Na temelju p i q izračuna se n = pq.
- Privatni ključ je (p, q), a javni ključ je n.
Algoritam za Rabinovo šifriranje otvorenog teksta javnim ključem glasi:
- Potrebno je dohvatiti javni ključ n.
- Poruka se prikaže kao cijeli broj x.
- Šifrat se izračuna pomoću formule eK(x) = x^2 mod n.
- Šifrat se pošalje primatelju.
Algoritam za Rabinovo dešifriranje šifrata privatnim ključem glasi:
- Potreban je privatni ključ (p, q).
- Pomoću algoritma za pronalaženje kvadratnih korijena modulo n kada su poznati njegovi prosti faktori izračuna se otvoreni tekst na temelju dobivenog šifrata. Više o ovom postupku može se pročitati u poglavlju 6.2 na poveznici http://www.mathos.unios.hr/~mdjumic/uploads/diplomski/ADA09.pdf.
Na poveznici https://asecuritysite.com/encryption/rabin2 moguće je isprobati šifriranje različitih poruka. Slika 4 prikazuje primjer šifriranja poruke „otorinolaringologija“ na navedenoj stranici.
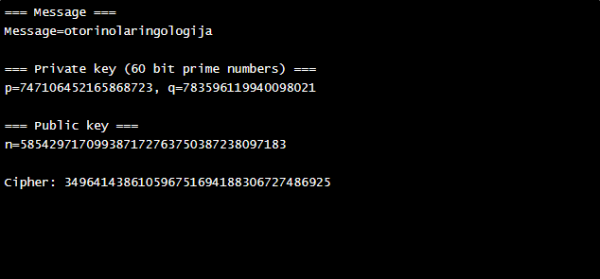
Slika 4: Primjer šifriranja poruke Rabinovim algoritmom na asecuritysite.com
6.3 ElGamalov kriptosustav
7. Napadi na kriptosustave s javnim ključem
8. Demonstracija kriptosustava s javnim ključem
9. Zaključak
10. Literatura
[1] https://hr.wikipedia.org/wiki/Kriptografija
[2] https://medium.com/@prashanthreddyt1234/real-life-applications-of-cryptography-162ddf2e917d
[3] https://hr.wikipedia.org/wiki/Kriptografija_javnog_klju%C4%8Da
[4] http://www.mathos.unios.hr/~mdjumic/uploads/diplomski/ADA09.pdf
[5] https://repozitorij.mathos.hr/islandora/object/mathos%3A251/datastream/PDF/view
[6] https://web.math.pmf.unizg.hr/~duje/kript/idejajavni.html
